Learn ZOE Math Practice Questions with Answers
This blog contains 21 math practice questions that Learn ZOE teachers prepared for you. The questions are based on different grade levels, and once the answer is revealed, there will be a detailed explanation of how we got the correct answer.
Feel free to answer the math practice questions first before revealing the answers.
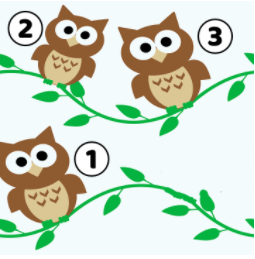
Kindergarten Questions
- Read the story.
There are 4 owls.
1 owl flies away.
How many owls were left?
Grade 1 Questions
2. Jack had 5 apples. He gave 2 to his friend. How many apples did he have left?
Jack gave 2 apples to his friends. Cross out two apples and count what’s left.
Jack has 3 apples left.
3. Which addition statement describes the array?
A.) 5 + 5
B.) 2 + 2 + 2 + 2 + 2
This array has 5 rows and 2 columns. This means the addition statement that describes the array is 2 + 2 + 2 + 2 + 2.
Grade 3 Questions
4. Question: The shape is made of unit squares. What is the area of the shape?
The area is measured in squares (or square units).
We can count the squares or we can take the length and width and use multiplication. The rectangle above has an area of 18 square units.
5. Allison is planning to plant lemons. If she has 24 lemon seeds and 8 pots and wants to plant an equal number of lemon seeds in each pot, how many lemon seeds will be planted in each pot?
Divide 24 by 8 to solve for the number of lemon seeds each pot will have.
Therefore, 3 lemon seeds will be planted on each pot.
Grade 4 Questions
6. Circle all the prime numbers.
87 \quad \quad \quad 57\quad \quad \quad 71 \quad \quad \quad 93 \quad \quad \quad 51 \quad \quad \quad 67
Prime numbers are numbers with only two factors—1 and itself.
87 = 290 x 3 or 1 x 87
57 = 19 x 3 or 1 x 57
71 = 1 x 71
93 = 31 x 3 or 1 x 91
51 = 17 x 3 or 1 x 51
67 = 1 x 67
Only 71 and 67 are prime.
Grade 5 Questions
7. A red ball is 58 inches across. A green ball is 524 inches across, and a blue ball is 512 inches across. List the balls in order from largest to smallest.
Change the fractions to fractions with like denominators by using 24 as the
LCD.
\frac { 5 \times 3 }{ 8 \times 3 } =\frac { 15 }{ 24 }
\frac { 5 \times 2 }{ 12 \times 2 } =\frac { 10 }{ 24 }
The balls must be arranged as red, blue, and green.
Note that the numerators of the original fractions are the same so we can
simply arrange the fractions according to their denominators—the smaller the
denominator, the bigger the value of the fraction.
8. Austin read 16of a book on the first day, 14the second day, and 13 on the third day. He was able to finish the book on the fourth day. What part of the book did Austin read on the fourth day?
Add all the fractions of the book Austin read using 12 as their common denominator.
\frac { 2 }{ 12 } +\frac { 3 }{ 12 } +\frac { 4 }{ 12 } =\frac {9}{12}\quad or\quad \frac {3}{4}
Since Austin read 1 whole book, subtract \frac {3}{4} from 1. Thus, Austin read \frac {1}{4} of the
book on the fourth day.
Grade 6 Questions
9. 3 cups of orange juice contain about 60 grams of sugar. How many cups of juice contain 80 grams of sugar?
3 cups of orange juice to 60 grams of sugar is 1:20 or 1 cup of orange juice to
20 grams of sugar. Therefore, 4 cups of orange juice contain 80 grams of sugar.
10. An exploration team pulls up a diver at a rate of 10 feet per minute. If the diver is 163 feet below sea level, represent the distance of the diver from sea level after 10 minutes using an integer.
up 10 x 10 = 100 feet. This means the diver is 63 feet below sea level after 10 minutes or -63.
Grade 7 Questions
11. Josh ate 70% of the whole cake. Mia ate 23 of the remainder. What percent of the cake is left?
1 whole pie is 100%. If Josh ate 70% of it, then 30% remained. Since Mia ate \frac { 2 }{ 3 }
of the remainder, \frac { 1 }{ 3 } was left. \frac { 1 }{ 3 } of 30% is 10%.
Grade 8 (Pre-Algebra) Questions
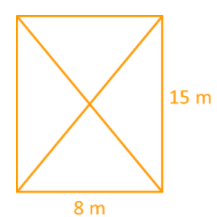
12. A worker needs to install diagonal braces on a wall. How long should each brace be if the wall is 15 meters high and 8 meters wide?
Each diagonal of a rectangle cuts the rectangle into two right triangles. Use Pythagorean Theorem to solve for the length
of each brace. Let x be the length of the braces.
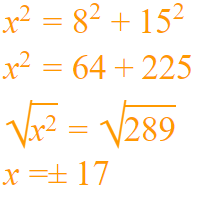We will choose the positive answer since x represents the length. Therefore,each brace must be 17 meters.
13. What is the probability that a card chosen from a standard deck will be a king or a spade? Express your answer in percent.
This is an A-or-B probability, where the events are not mutually exclusive. This means that the two events (king or spade) can happen independently and
there is a probability that the card will be a king and at the same time a spade.
We can use the formula:
P(A or B)=P(A)+P(B)-P(A and B)
P(King or Spade)=P(King)+P(Spade)-P(King of Spades)
P(A or B)=452+1352-152
P(A or B)=413 or about 31%
Thus, the probability that the card is chosen from a standard deck of cards is
a king or a spade is 31%.
Algebra 1
14. 36 grams of mixed nuts contain 35% cashew nuts. Other mixed nuts weigh 48 grams and contain 42% cashew nuts. What percent of the new mixture are cashews if the two mixed nuts are mixed?
Let x be the percent of the cashew nuts in the mixture. Organize all the information using a table.
| Mixture 1 + Mixture 2 | Result | ||
|---|---|---|---|
| Concentration | 0.35 | 0.42 | x |
| Amount | 36 | 48 | 84 |
| Product | 12.6 | 20.16 | 84x |
Based on the given information, our equation is 12.6+20.16=84x. Therefore, x=0.39 or the new mixture has 39% cashew.
15. The table shows a city’s population every 10 years since 1960. Use the quadratic regression that best fits the data to approximate the population in 2009.
| Number of Years since 1960 | Population (in thousands) |
| 0 | 501 |
| 10 | 903 |
| 20 | 1423 |
| 30 | 1874 |
| 40 | 3100 |
| 50 | 4123 |
Solve for the quadratic model using a graphing calculator or any graphing
utility. Follow the steps below to use the TI-84 Plus CE Graphing Calculator.
- Press STAT button and choose 1: Edit…
- Enter the data for the number of years under L1 and the population
under L2. - Press STAT button again and choose CALC.
- Under CALC, choose 5: QuadReg
- The Xlist and Ylist will automatically have the L1 and L2.
Choose Calculate. - The calculator will give you the values of a, b and c.
The equation of best fit is y = 1.06x^2 + 18.93x + 543.68. Using the
equation of best fit, approximate the population in 2009. From 1960 to
2009 is 49 years. Plug in 49 into the equation and solve for y.
y = 1.06(49)^2+18.93(49)+543.68
y\approx 4016
Thus, the population in 2009 was about 4,016,000.
Geometry
16. Find the values of x and y. Assume the segments that appear to be tangent are tangent.
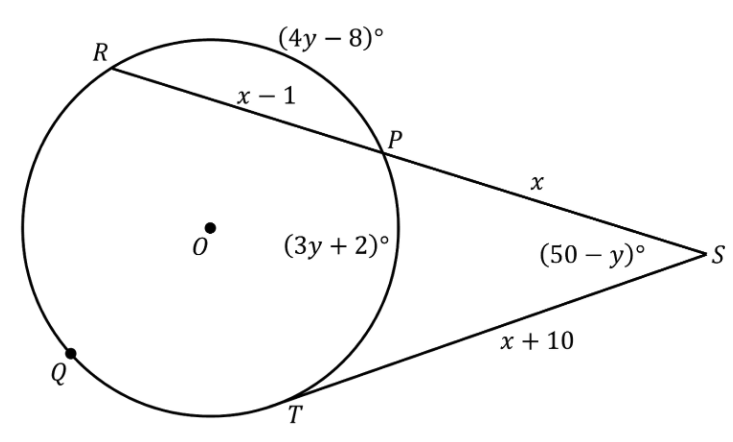
Figure not drawn to scale.
To solve for x, we use the fact that the product of the secant segment and its external segment is equal to the square of the tangent segment. Since
RS=x+(x-1),
RS · PS = (TS)^2
x(2x - 1) = ( x + 10)^2
2x^2 - x = x^2 + 20x + 100
x^2 - 21x - 100 = 0
( x + 4)(x - 25) = 0
x = -4 or x=25.
We will choose the positive value of x since it represents the length.
To solve for y, use the fact that the measure of the angle formed by a secant
and a tangent drawn from a point outside a circle is equal to half the difference
of the measures of the intercepted arcs. That is,
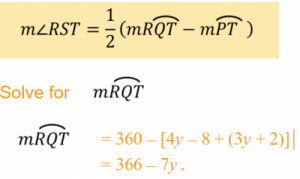
Substitute values into the equation.
\begin{alignedat}{2}50-y&=\frac { 1 }{ 2 } \left[ 366-7y-\left( 3y+2 \right) \right] \\ 50-y&=\frac { 1 }{ 2 } \left[ 364-10y \right] \\ 50-y&=182-5y\\ 4y&=132\\ y&=33\end{alignedat}
Thus, x=25 and y=33.
Algebra 2
17. Question: Find the solution(s) to the equation \sqrt { 2x - 1 } - \sqrt { x - 1 } = 5.
Eliminate one radical expression at a time. Eliminate \sqrt {2x-1} then simplify
the equation.
\begin{alignedat}{2} \sqrt {2x - 1} &= 5 + \sqrt {x - 1} \\ (\sqrt {2x - 1)^2} &= (5 + \sqrt {x-1})^2 \\ 2x - 1 &= 25 + 10 \sqrt {x - 1} + x - 1 \\ x - 25 &= 10 \sqrt {x - 1}\end{alignedat}
Eliminate \sqrt {x - 1} then solve for x.
\begin{alignedat}{2}\sqrt {x - 1} &= \frac {x - 25}{10} \\ (\sqrt {x - 1})^2 &= (\frac{x-25}{10})^2 \\ x - 1 &= \frac{x^2 - 50x + 625}{100} \\ -50x + 625 &= 100x - 100 \\ x^2 - 150x + 725 &= 0 \\ (x - 145)(x - 5) &= 0 \end{alignedat}
\quad x = 145 or x = 5
Check for extraneous solutions.
\begin{alignedat}{2}\sqrt {2(145) - 1} - \sqrt {145 - 1}&≟ 5 \\ \sqrt {289} - \sqrt {144}&≟ 5 \\ 17 - 12 &≟ 5 \\ 5 &= 5 True\end{alignedat}
\begin{alignedat}{2}\sqrt {2(5) - 1} - \sqrt {5 - 1}&≟ 5 \\ \sqrt {9} - \sqrt {4} &≟ 5 \\ 3 - 2 &≟ 5 \\ 1 &≠ 5 False\end{alignedat}
Therefore, the only solution to the equation is x=145.
18. Question: A ball is dropped from a height of 20 meters. Each time the ball hits the ground, it bounces to 34 of its previous height. On which bounce will the ball have traveled 90% of the total distance?
The total distance d travelled by the ball makes an infinite geometric series
of its down-up bounces:
d=20+20\left( \frac { 3 }{ 4 } \right) +20\left( \frac { 3 }{ 4 } \right) +20{ \left( \frac { 3 }{ 4 } \right) }^{ 2 }+20{ \left( \frac { 3 }{ 4 } \right) }^{ 2 }+20{ \left( \frac { 3 }{ 4 } \right) }^{ 3 }+20{ \left( \frac { 3 }{ 4 } \right) }^{ 3 }+...\\ d=20+40\left( \frac { 3 }{ 4 } \right) +40{ \left( \frac { 3 }{ 4 } \right) }^{ 2 }+40{ \left( \frac { 3 }{ 4 } \right) }^{ 3 }+...
We can also rewrite this with -20 so that the first term is also 40 and express
the series using sigma notation.
d=-20+40{ \left( \frac { 3 }{ 4 } \right) }^{ 0 }+40\left( \frac { 3 }{ 4 } \right) +40{ \left( \frac { 3 }{ 4 } \right) }^{ 2 }+40{ \left( \frac { 3 }{ 4 } \right) }^{ 3 }+...\\ d=-20+\sum _{ n=0 }^{ \infty }{ 40 } { \left( \frac { 3 }{ 4 } \right) }^{ n }
We can now solve for the total distance traveled by the ball using the formula
for finding the sum of a converging infinite geometric series.
\begin{alignedat}{2}d&=-20+\frac { 40 }{ 1-\frac { 3 }{ 4 } } \\ d&=-20+\frac { 40 }{ \frac { 1 }{ 4 } } \\ d&= -20+160\\ d&=\quad 140\quad meters \end{alignedat}
To solve for the bounce n on which the ball will have traveled 90% of the
distance, we will use the formula for finding the partial sum of finite geometric series.
\begin{alignedat}{2}09\left( 140 \right) &=-20+40\left( \frac { 1-{ \left( \frac { 3 }{ 4 } \right) }^{ n } }{ 1-\frac { 3 }{ 4 } } \right) \\ 126&=-20+160\left[ 1-{ \frac { 3 }{ 4 } }^{ n } \right] \\ 126&=-20+160-160{ \left( \frac { 3 }{ 4 } \right) }^{ n }\\ -14&=-160{ \left( \frac { 3 }{ 4 } \right) }^{ n }\\ { \left( \frac { 3 }{ 4 } \right) }^{ n }&=\frac { 7 }{ 80 } \\ n&=\log { 0.75 } \left( 0.0875 \right) \\ n&\approx 8\end{alignedat}
Thus, the ball will have bounced 90% of the total distance after about
8 bounces.
Precalculus/Math Analysis
19. What are the equations of the asymptotes of \frac { { \left( x-4 \right) }^{ 2 } }{ 256 } -\frac { { \left( y+1 \right) }^{ 2 } }{ 324 } =1 ?
The given equation is an equation of a hyperbola of the form
\frac { { \left( x-h \right) }^{ 2 } }{ { a }^{ 2 } } -\frac { { \left( y-k \right) }^{ 2 } }{ { b }^{ 2 } } =1. This indicates that the hyperbola has a horizontal
tranverse axis. Thus, the formula for the asymptotes of a horizontal hyperbola
is
y=k\pm \frac { b }{ a } \left( x-h \right) .
Find the values of the variables using the given equation then plug them into
the formula.
h= 4
k= -1
a= 16
b= 18
y = -1 + \frac {18}{16}(x - 4).
y = -1 + \frac {9}{8}x - \frac {9}{2}
y = \frac {9}{8}x - \frac {11}{2}
y = -1 - \frac {18}{16}(x - 4)
y = -1 - \frac {9}{8}x + \frac {9}{2}
y = - \frac {9}{8}x + \frac{7}{2}
20. Question: Solve for the solutions to tan(x - \frac {π}{3}) - sin^2(x) tan(x - \frac {π}{3}) = 0 on the interval [0,2π).
Factor out tan(x - \frac {π}{3})
tan(x - \frac {π}{3})[1 - sin^2(x) = 0
Solve each part separately. tan(x) is equal to zero when x = 0 + πk
tan( x - \frac {π}{3}) = 0
x - \frac {π}{3} = 0 + \frac {π}{k}
x = \frac {π}{3} + πk
Find the values of k for which the equation is defined on the required interval.
When k= -1, x = -\frac {2π}{3}. This is out of the interval.
When k= 0, x = \frac {π}{3}. This is on the interval so it is included in the solution.
When k= 1, x = \frac {4π}{3}. This is on the interval so it is included in the solution.
k cannot be more than 1 otherwise the value of x will be out of the interval.
Solve 1 - sin^2(x) = 0. Use the trigonometric identity
sin^2(x) + cos^2(x) = 1 to solve.
1 - sin2(x) = 0
cos^2(x) = 0
\sqrt {cos^2(x)} = \sqrt {0}
cos(x)=0
x = \frac {π}{2}, \frac {3π}{2}
Thus, the solution to the equation on the interval are \frac {π}{2}, \frac {3π}{2}, \frac {π}{3} and \frac {4π}{3}.
AP Calculus AB/BC
21. Question: Find the coordinates of the points where local maxima or minima are located within f(x) = x^4 + 12x^3 - 3.
The local extrema of a function are located at the points where the first
derivative of the function is equal to zero or is undefined. We can solve for
the local extrema using the First Derivative Test.
f'(x) = 4x^3 + 36x^2
Set the derivative equal to zero and solve for x.
4x^3 + 36x^2 = 0
4x^2(x + 9) = 0
x = 0 and x = -9
Test whether the value of the first derivative changes from left to right
between each value of x.
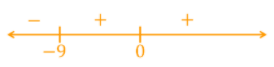
When the value of the derivative changes from left to right between the
value of x, a local extremum exists. Between -9, the value of the derivative
changes from negative to positive. This means a local minimum exists.
Between 0, the value of the derivative doesn’t change. This means there’s
no local extremum at x=0.
Plug in -9 into the function to find the y-coordinate of the local minimum.
y = (-9)^4 + 12(-9)^3 - 3
y = -2190
Thus, the coordinates of the local minimum of the function are (-9, -2190).
