Simplifying Fractions

What is a Fraction?
A fraction represents a part of a whole. It describes equal parts of an object or a group like one-half, one-fourth, two-eighths, etc. For example, a slice of pizza is a fraction of the whole pizza. Some of these fractions can be simplified and we call this method simplifying fractions.
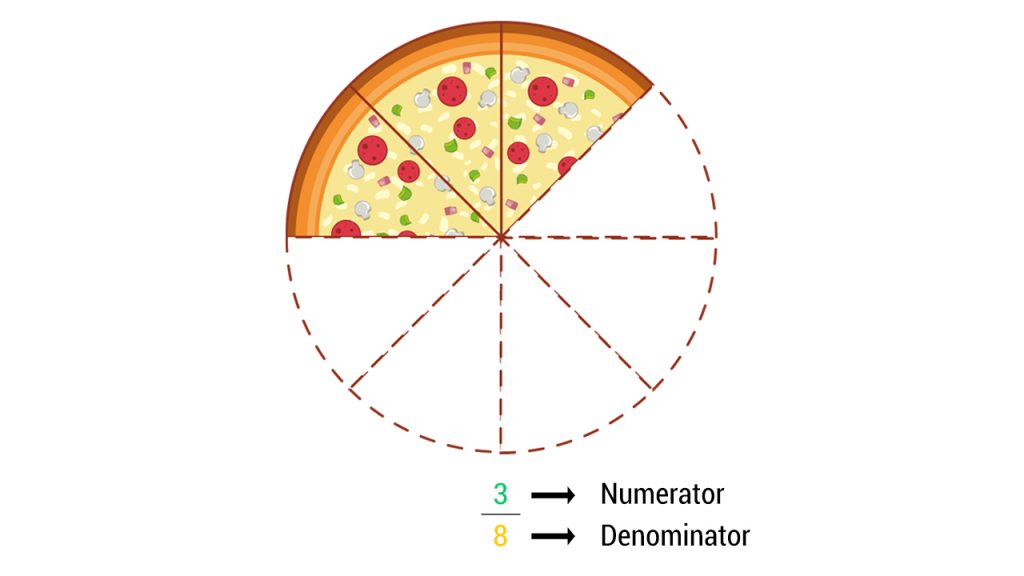
The top number (numerator) tells us how many parts we have. The bottom number (denominator) tells us the total number of parts an object is divided into. In our example, we have 3 slices (numerator), and the pizza is divided into 4 slices (denominator).
Some fractions are equivalent fractions. These fractions seem different from each other but they are actually equal! For example, \frac { 4 }{ 8 } and \frac { 1 }{ 2 } are equivalent fractions because they have the same size as shown below.
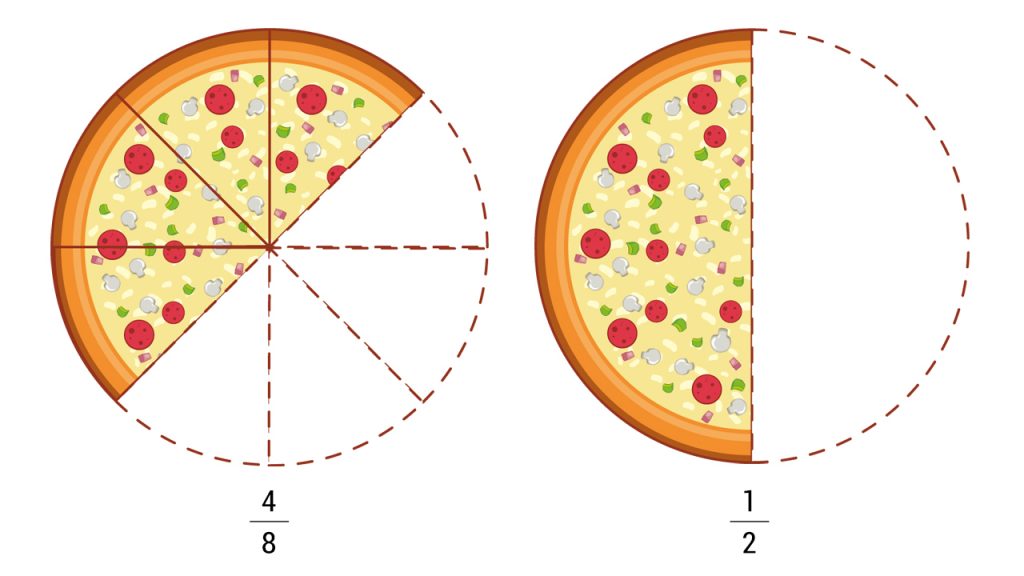
\frac { 1 }{ 2 } is the simplified form of \frac { 4 }{ 8 }. Simplifying fractions mean that we want to reduce a fraction to its simplest form as possible. We will talk about two ways to simplify fractions.
Method 1 in Simplifying Fraction with Common Number
We can simplify fractions by dividing both the numerator and the denominator by a common number without remainders. Repeat the process by another number until you reach the smallest whole number.
Example: Simplify \frac { 64 }{ 72 }.
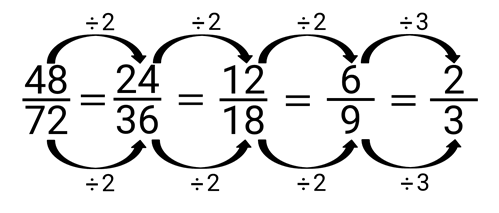
\frac { 48 }{ 72 } is divided by 2 three times and then divided by 3 to get \frac { 2 }{ 3 }. This is the simplest form of the fraction.
This works for all fractions you need to simplify. Another interesting way to do this method is the division ladder method.
First, write 48 and 72 inside an upside-down long division symbol. This becomes the first ladder.
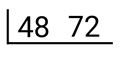
Then, think of a common factor of 64 and 72. Let’s use 2 since 64 and 72 are divisible by 2. You can use other bigger common factors that you can think of. Divide both numbers by two, write the quotients under the division symbol and create another division symbol for the second ladder.
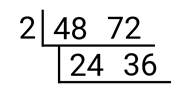
Think of other common factors of 32 and 36 to use to divide both. We can still use 2 since both are even numbers. 2 is the easiest number to start with when you are dividing even numbers, but you can use bigger factors other than 2 for as long as it is a common factor of the numerator and the denominator. Repeat the process until the common factors of the quotient is 1.
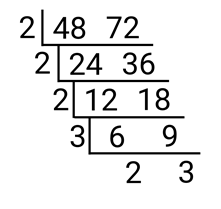
The last quotients are the numerator and denominator of the reduced fraction. The division ladder is one of the easiest and fastest ways to simplify fractions if you can’t think of bigger factors to use to divide the numerator and denominator. This will also give you the GCF of the numbers. Just multiply all the factors you used to divide the two numbers.
2\quad \times \quad 2\quad \times \quad 2\quad \times \quad 3\quad =\quad 24
Method 2 Simplifying Fraction with Greatest Common Factor
Divide the numerator and the denominator by its Greatest Common Factor (GCF). There are two ways to find the GCF—listing the factors of the two numerators and denominator and prime factorization.
Example 1: Simplify \frac { 36 }{ 60 }.
List all the factors of 36 and 60, then find their GCF.
36\quad \rightarrow \quad 1,\quad 2,\quad 3,\quad 4,\quad 6,\quad 9,\quad 12,\quad 18,\quad 36
60\quad \rightarrow \quad 1,\quad 2,\quad 3,\quad 4,\quad 5,\quad 6,\quad 10,\quad 12,\quad 15,\quad 20,\quad 30,\quad 60
Divide the numerator and the denominator by their GCF.
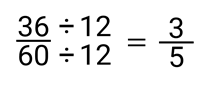
Sometimes, listing the factors of the numbers to find the GCF is a little tedious. Using prime factorizations such as factor tree is easier for bigger numbers.
Example 2: Simplify \frac { 64 }{ 120 }.
Find the GCF of 64 and 120 by using prime factorization. Let’s use the factor tree to list all the prime factors of the two numbers.
First, find two factors of 64 and 120. We can use 8 \times 8 for 64 and 12\times10 for 120. Write them down as branches.

Factor out 8, 12, and 10 for new branches. Repeat the process until you only have their prime factors.
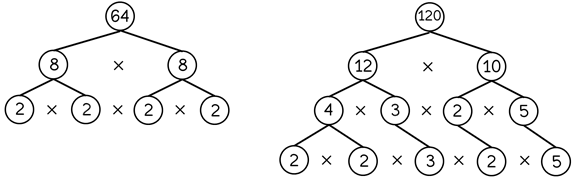
List the prime factors of 64 and 120 and list the common prime factors they have. The product of the common factors is their GCF.
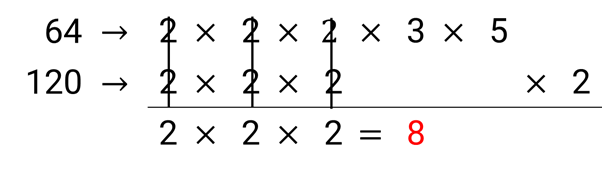
Divide 64 and 120 by 8 to simplify the fraction.
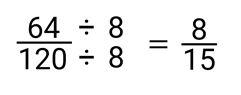
Simplifying fractions will always come in handy especially when learning a higher degree of Mathematics. It’ll be used more often than other math concepts. Factorization skills are essential in simplifying fractions. We recommend mastering the basic facts of multiplication and division to help you with factoring.


