Equivalent Fractions

Equivalent fractions represent the same size even if the numbers look different. Let’s take a look at the pizzas below.
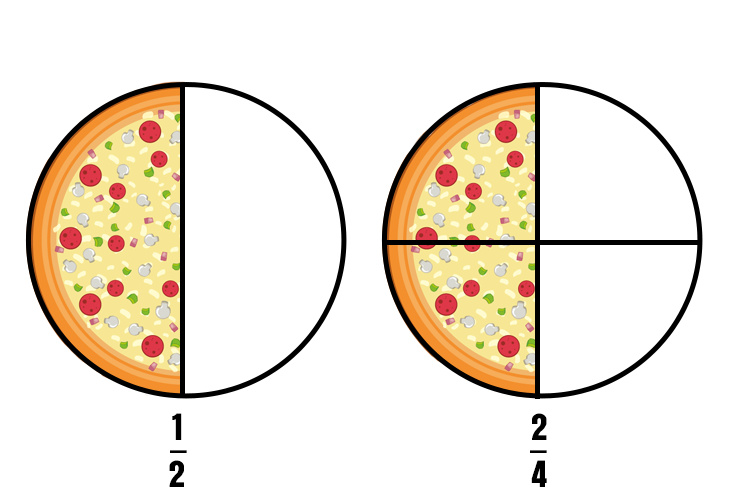
The two fractions have different numerators and denominators but represent the same size of pizza slices. \frac{2}{4} when simplified, is actually \frac{1}{2} . It is important to remember that these two fractions still represent two different ways the wholes are partitioned. \frac{1}{2} means the whole is divided into two equal parts, while \frac{2}{4} means a whole divided into four parts.
Finding Equivalent Fractions
Learning how to create and identify equivalent fractions is an important bridge to learning simplifying fractions. Remember this rule:
“Multiply or divide the top and bottom with the same number!”
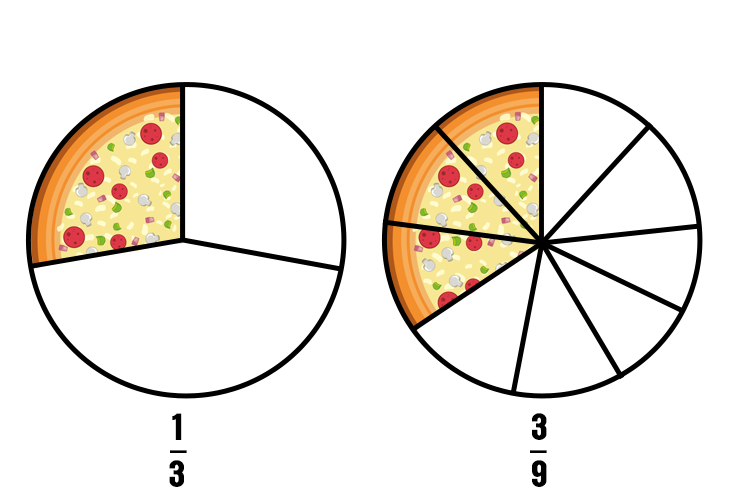
When we multiply a fraction’s numerator and denominator by the same number, we get an equivalent fraction. For example, let’s make a fraction equivalent to \frac{1}{3} .
\frac{1\times3}{3\times3}= \frac{3}{9}
We multiplied the numerator and denominator of \frac{1}{3} by 3 to get \frac{3}{9}. The two pizzas below show that they are indeed equivalent.
To identify whether the two fractions are equivalent using multiplication, use a number to multiply the numerators and denominators. The product is the equivalent fraction.
\frac{2}{5} and \frac{10}{50}
The two fractions above are equivalent because we can multiply 2 and 5 of \frac{2}{5} by 10 to get \frac{10}{50}.
Dividing a fraction’s numerator and denominator to make two fractions equal is the basic concept of simplifying fractions. For example,
\frac{4\div4}{8\div4}= \frac{1}{2}
When 4 and 8 of \frac{4}{8} are divided by 4, we get \frac{1}{2} which is the simplified form of \frac{4}{8}. Both are equivalent, as shown below.
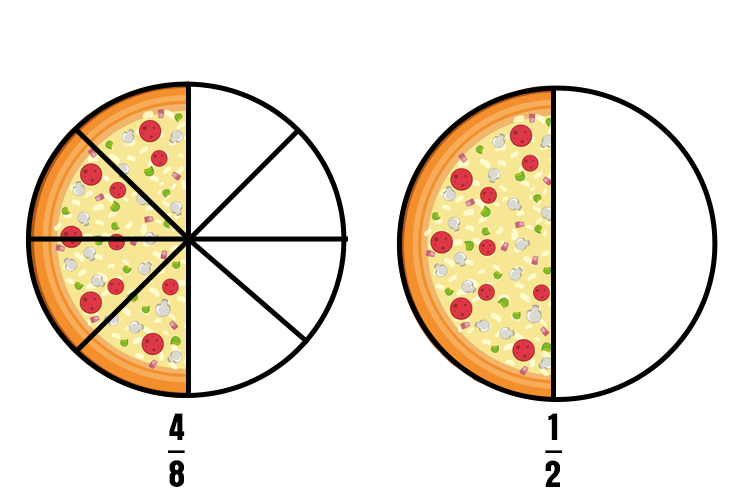
We can also divide 4 and 8 of \frac{4}{8} by 2 to get \frac{2}{4}. Both are also equivalent. You will get two equivalent fractions if you divide by the same number. Learning divisibility rules and mastering multiplication and division basic facts will help you create and identify this type of fraction.
Fractions Wall Charts
Explore more examples of fractions using the following charts. Have fun!
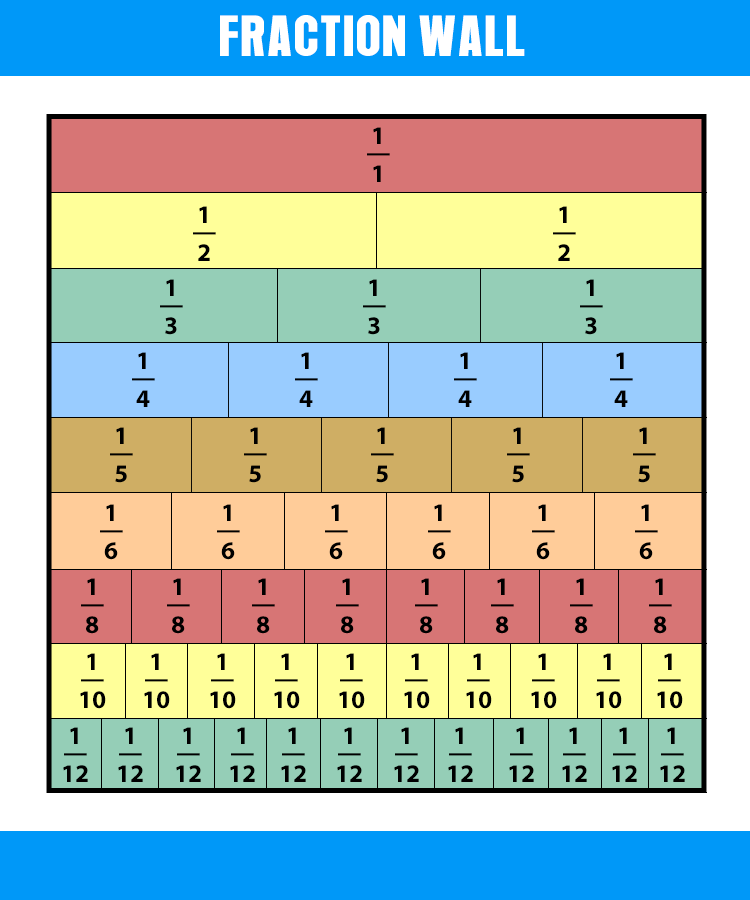
In the fraction wall, we can see that \frac{1}{2} is equivalent to \frac{2}{4},\frac{3}{6},\frac{4}{8}, etc. We multiply 1 and 2 by 2 to get \frac{2}{4}, by 3 to get \frac{3}{6}, and by 4 to get \frac{4}{8}. We can also do the opposite. Divide the numerators and denominators of the fractions by those same numbers to get \frac{1}{2}.

The 2nd and 3rd-grade multiplication chart can also help us create and identify the type of fractions. The first column shows the fractions in different colors. The first row is the multipliers. For example, \frac{1}{2} can be multiplied by 2, 3, 4, etc., to create the fractions equivalent to it.
Summary
- Equivalent fractions are fractions with different numerators and denominators but represent the same size.
- We can only multiply or divide a fraction’s numerator and denominator to identify whether fractions are equivalent.
- Divisibility Rules is a helpful trick, while multiplication and division basic facts are essential skills to learn.
- Learning equivalent fractions is a bridge to mastering simplifying fractions.


