Adding and Subtracting Fractions

Adding and Subtracting fractions may seem a terrifying Math lesson for some, but the truth is it is not as complicated as some people might think. The trick is to be able to recognize and translate fractions into familiar objects; which is why pizza slices and chocolate bars are commonly used to represent fractions. This way you can visualize the fraction and understand the fraction easily.
Addition of Fractions: How Do You Add Fractions?
Let’s say you and your friend each have \frac { 1 }{ 4 } of a pizza.
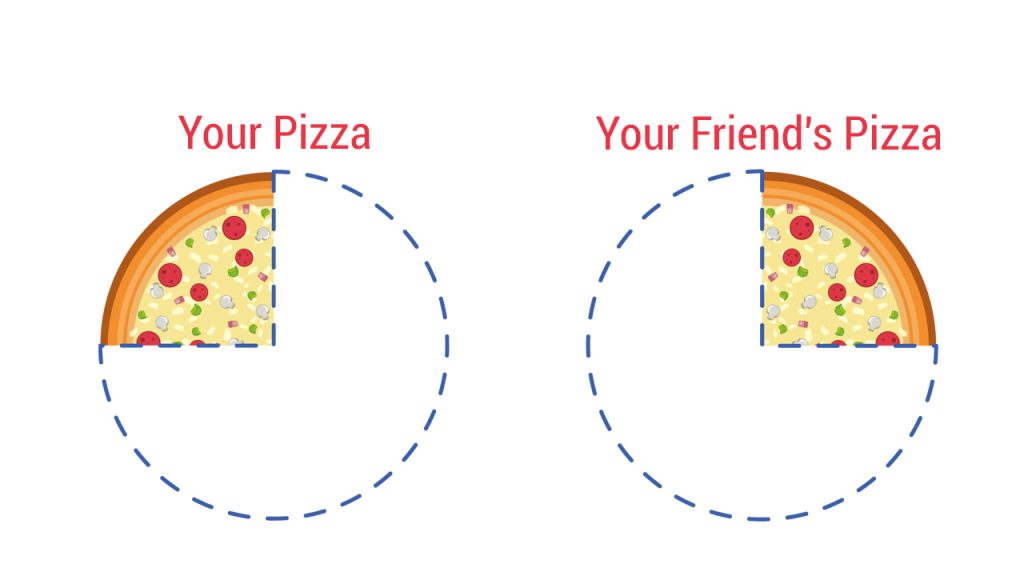
Adding them up, the sum is \frac { 4 }{ 8 } of the pizza which is also equal to ½ of the pizza when you simplify.
\frac { 1 }{ 4 } +\frac { 1 }{ 4 } =\frac { 2 }{ 4 } =\frac { 1 }{ 2 }
Notice that the numerators (numbers on top of a fraction) are the only numbers that are added. The denominators (numbers at the bottom of a fraction) are never added together. When you add fractions, it is important to make sure that the denominators are the same. The reason for this is that similar denominators tell you that the fractions you are adding are divided into similar portions.
Let’s take these pizza slices as an example. Say you have \frac { 1 }{ 4 } pizza and your friend has \frac { 2 }{ 4 } of the same pizza.
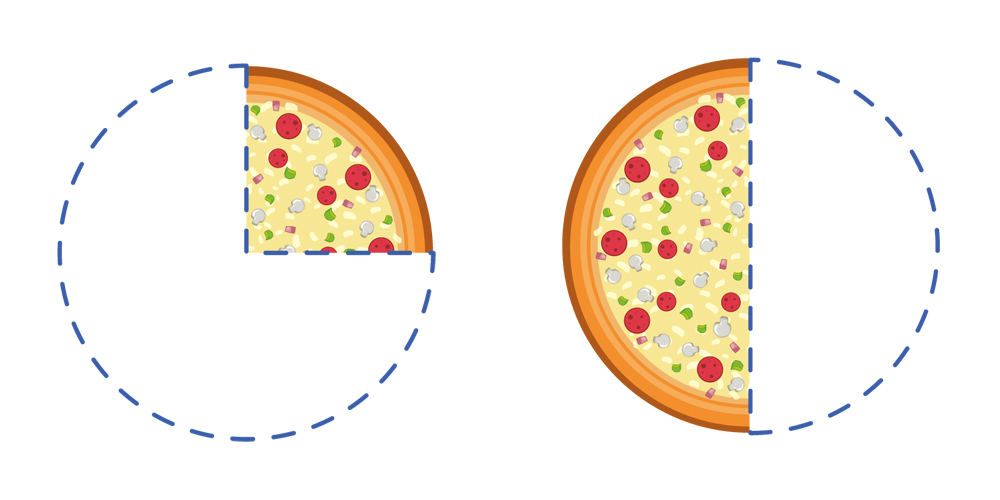
We know that \frac { 1 }{ 2 } pizza can be sliced in two equal parts so that they are similar portions. By doing so, it becomes 3 slices of \frac { 1 }{ 4 } sized pizza. This gives us:
\frac { 1 }{ 4 } +\frac { 2 }{ 4 } =\frac { 3 }{ 4 }
Adding fractions is only possible if the denominators are the same because you can only combine accurately if you add similar portions. That is why the first rule of adding fractions is making sure the denominators of your addends are the same because they represent how many equal portions the fractions were divided into.
Subtracting Fractions: How Do You Subtract Fractions?
The same rule applies when subtracting fractions. The numerators are subtracted and the denominators must be similar.
Let’s say you have \frac { 5 }{ 8 } of a chocolate bar and you ate \frac { 1 }{ 8 }
\frac { 5 }{ 8 } -\frac { 1 }{ 8 } =\frac { 4 }{ 8 } of the chocolate bar and \frac { 4 }{ 8 } can be simplified as \frac { 1 }{ 2 } .
Adding and Subtracting Fractions with Unlike Denominators
When adding and subtracting fractions with denominators that are not similar, the first step is to make the denominators similar. To do this, you need to find the equivalent fraction of each addends while making sure that both addends are similar. You may use any common denominator but using the least common denominator makes addition and subtraction not only easier but also simpler.
Here are some examples:
Example 1: Adding Fractions
\frac { 1 }{ 3 } +\frac { 2 }{ 5 } =Step 1: Make the denominators similar by finding the least common denominators. Solving for the least common denominator is the same as solving for the least common multiple.
List down the multiples of 3 and 5 . The first multiple that they have in common is the least common multiple.
3: 3, 6, 9, 12, 15, 18
5: 5, 10, 15, 20
Least Common Multiple: 15
Use the least common multiple as your least common denominator.
Step 2: Rename the addends by finding the equivalent fractions of each addend using the least common denominator.
\frac { 1 }{ 3 } becomes:
\frac { 1 }{ 3 } \times \frac { 5 }{ 5 } =\frac { 5 }{ 15 }
\frac { 2}{ 5 } becomes:
\frac { 2 }{ 5 } \times \frac { 3 }{ 3 } =\frac { 6 }{ 15 }
Step 3: Add the renamed fractions
\frac { 5 }{ 15 } +\frac { 6 }{ 15 } =\frac { 11 }{ 15 }Example 2: Subtracting Fractions
\frac { 4 }{ 5 } -\frac { 1 }{ 2 } =Step 1: Make the denominators similar by finding the least common denominators.
List down the multiples of 5 and 2. The first multiple that they have in common is the least common multiple.
5: 5, 10, 15, 20
2: 2, 4, 6, 8, 10
Least Common Multiple: 10
Use the least common multiple as your least common denominator.
Step 2: Rename the addends by finding the equivalent fractions of each addend using the least common denominator.
\frac { 4 }{ 5 } becomes:
\frac { 4 }{ 5 } \times \frac { 2 }{ 2 } =\frac { 8 }{ 10 }\frac { 1 }{ 2 } becomes:
\frac { 1 }{ 2 } \times \frac { 5 }{ 5 } =\frac { 5 }{ 10 }Step 3: Subtract the renamed fractions
\frac { 8 }{ 10 } -\frac { 5 }{ 10 } =\frac { 3 }{ 10 }Adding and Subtracting Fractions is not rocket science. Understanding the numerator and the denominator is the first step in solving these two operations corrections. It is also helpful to master the basic facts of multiplication as it is most useful when making the denominators similar.


